融合理工学系 News
山下研究室-研究室紹介 #13-
人類の未来を拓く知見の創造・技術の開発
研究室紹介シリーズでは、ひとつの研究室にスポットを当てて研究テーマや研究成果を紹介します。今回は、人類福祉の向上を目指した技術開発,人類に新しいものの考え方を提供する科学的知見の創造の研究を行う、山下研究室です。
| 研究分野 | パターン認識 / 機械学習 / 画像処理 |
|---|---|
| 研究キーワード | 変形に頑健なマッチング / 局所独立方程式 /ウエーブレット画像符号化 |
| Webサイト | 山下研究室 |
研究室のアピールポイント
大学が果たすべき役割の中で最も重要なものは、学問を作ることです。学問は人をその他の動物と分けるものですし、非合理的で単なる過去からのしがらみのような思想、ものの見方から人を自由にするものです。このような考えのもと、本研究室では人間の知能をコンピュータ上に実現することを目指して、新しい学問のもとになる「知見」を創造するための研究、さらに画像を対象として、その知見をもとに現実の社会に役立つ「技術」を生み出していく研究を行っています。
研究室所属学生は、線形代数学、解析学、微分幾何学、確率・統計学に基づいて、機械学習、パターン認識、画像処理のための理論を構築する研究、グラフィックプロセッシングユニット(GPU)を利用して並列計算を実行するためのプログラミングを行う研究などを自由な雰囲気の中で行っています。そして、新型コロナウイルスの影響を最小限にするために、研究室の計算資源を外部から安全に利用できる環境を整えると共に、遠隔会議のためのサーバーを研究室内に設置し学生が自由に使えるようにして研究を推進しています。
研究テーマ
パターン認識
人間の知能をコンピュータ上に実現する上で、パターン認識は最も基本的なものです。この技術は、古くは1970年ごろから郵便区分機の実現のために使われています。これは、郵便番号を画像から読み取り、郵便番号ごとに郵便を自動的に振り分けるものです。その他にも、ディジタルカメラの顔検出、画像から物体を探してくる画像マッチングなどに使われています。しかし、その性能はまだ十分とは言えません。例えば、1998年に郵便番号を5桁から7桁にした理由は、手書き漢字認識の精度が低かったからです。1998年以前の郵便番号は郵便局に対する、5桁の番号でした。省力化を進めるため、住所をコンピュータで読み取ろうとしましたが、漢字を精度良く読み取ることができなかったため、郵便番号を7桁に拡張して、住所の数字以外の部分(町域)までを表すようにしたのです。本研究室では、変形に頑健なマッチング、画像特徴量や、それらを用いた認識、さらに、それらの高速な計算法に関して研究を行っています。

機械学習
人間の知能をコンピュータ上に実現する場合、その動作の全てをプログラムで書くことは現実的には不可能です。従って、現実のデータをコンピュータに学習させて、高度な知能を獲得するようにする必要があります。そのための機械学習では、一般にはまずモデルを決め、そのモデルのパラメータを獲得する方法に関して論じていきます。この学習の方法は、一見人間の学習とは関係なさそうに見えます。しかし、人間の脳における学習も神経細胞間で信号を伝えるシナプスの結合強度を調整することによって行われており、パラメータを調整しているとも言えます。本研究室では、多様体上の正規分布に基づく学習理論、カーネル法の拡張、事後確率を求めずに事後確率を最大にする関数を求める学習モデルとパラメータの計算方法に関して研究を行っています。
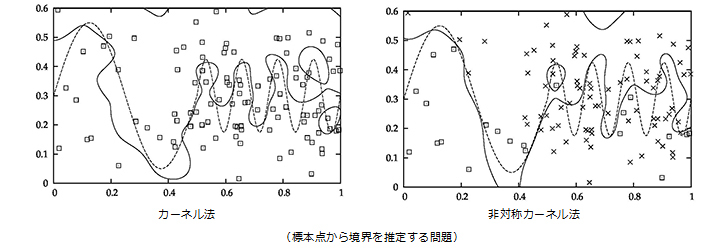
画像・映像符号化
画像を使ったコミュニケーションは、円滑なコミュニケーションのために非常に重要です。しかしながら、画像のデータは膨大です。ハイビジョン画像は、1920x1080画素からなります。1画素は赤・青・緑の光の強さの値から構成されます。その光の強さの値を256レベルで表すとすれば8 bitのデータ量が必要です。その画像を毎秒30枚送るとすれば必要なデータ通信速度は、1920 x 1080 x 3 x 8 x 30 = 1492992000 ≒ 1.5 Gbit/sとなります。しかも今後、4Kテレビ(3840 x 2160画素)、8Kテレビ(7680 x 4320 画素)と画素数が増え、送らなくてはいけないデータ量は増加していきます。画像・映像符号化の目的は、画像をできるだけ劣化させることなく、このデータ量を削減することです。単にデータ量を削減すると、復号画像にブロックが見えるというブロック歪や、エッジの周辺の明度が振動するというリンギングの問題が生じます。この問題を解決するために、本研究室ではウエーブレット画像符号化にライン予測を導入して、高効率な画像符号化を目指しています。


研究成果/研究詳細
変形に頑健なマッチング
文字を観測する場合、観測する角度によって射影変換によって変形した文字が画像として得られます。また、手書き文字は書き手によって様々に変形しますが、その変形の大きな部分は射影変換によって与えられると言われています。画像マッチングでは、まず特徴点を抽出し、点同士を対応させる方法が一般的です。しかし、特徴が少ない画像、ボケたりブレたりした画像では、特徴点の抽出が困難になります。領域全体をマッチングする領域マッチングには、このような問題がなく、最終的なマッチング精度が高いという利点があります。この領域マッチングに基づき、局所特徴フィルタを評価基準に取り入れ、射影変換に頑健なマッチング手法を開発しました。それを手書き数字認識に適用し、MNIST手書き数字データベースを用いた認識実験で、99.7%という深層ニューラルネットワーク以外ではほぼ最高の性能を出しています。

- 10,000個のテストパターンに対して、99.7%の認識率を達成したときに、
誤認識した30個のパターン(矢印左側数字が真値、右側が認識結果)
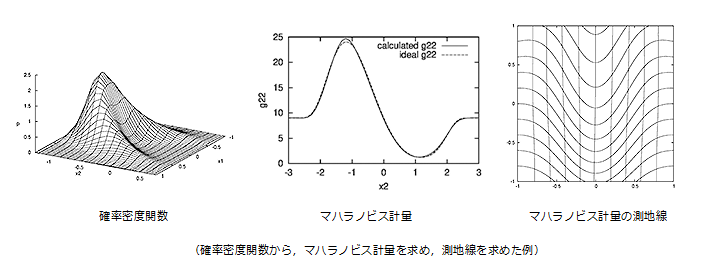
マハラノビス計量
パターンが同じカテゴリーに属するかどうか評価するためにはパターン間の距離を定義する必要があります。例えば、2つのパターンが通常の距離であるユークリッド距離で遠いと評価される場合でも、パターンが変形しやすい方向に離れている場合には近いと評価することが必要です。逆に、変形しにくい方向には遠いと評価することが必要になります。このような確率に基づいた距離を可能にするために、多様体上の正規分布を定義する局所等方独立方程式を計量に関する方程式と読み替え、マハラノビス計量方程式によってマハラノビス計量を定義することを可能にしました。また、特徴抽出などに利用するために、マハラノビス計量を使った次元削減法を開発しています。
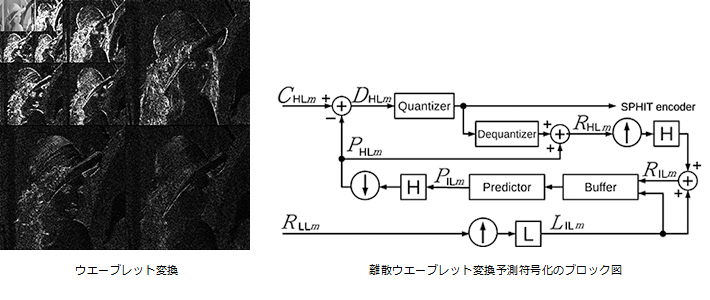
離散ウエーブレットに基づくニューラルネットワークによる予測符号化
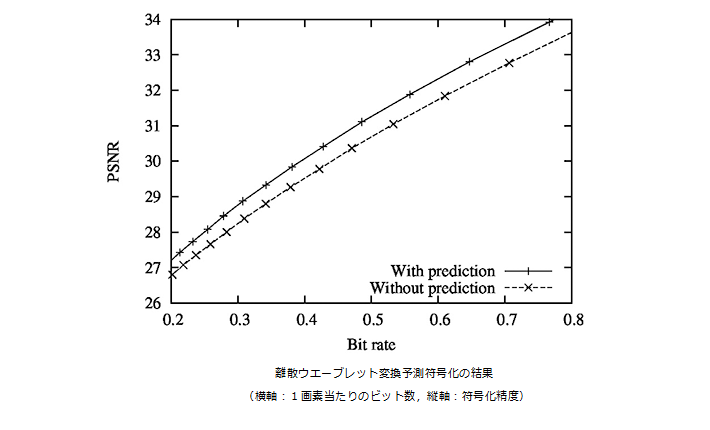
現在使われている画像符号化方式であるJPEGや映像符号化方式MPEGでは、ブロック変換である離散コサイン変換が使われていますが、ブロック変換であるために復号画像にブロック歪が生じます。離散ウエーブレット変換に基づく画像符号化は、このブロック歪が生じることなく、符号化効率が高いことが知られています。画像符号化における離散ウエーブレット変換では、1ラインずつ変換を行います。そのため、現在符号化するラインより上のラインの信号は復号可能で、符号化するラインの予測に使うことができます。そうすれば、そのラインの信号自体でなく、予測が外れた分だけの情報を送れば良いため、データ量を削減することができます。この予測にニューラルネットワークを用いることによって、符号化効率を高めることを可能としています。
出版リスト
代表論文:
- [1] 山下幸彦, 若原徹 , “画像領域マッチングのための目標領域特徴量による初期位置探索法,” 電子情報通信学会論文誌 D, vol. J103-D, no. 4, pp.330-340, April, 2020 DOI:10.14923/transinfj.2019JDP7056

- [2] C. N. Ochotorena and Y. Yamashita, “Anisotropic guided filtering,” IEEE Transactions on Image Processing, vol. 29, pp.1397-1412, 2020. DOI:10.1109/TIP.2019.2941326

- [3] Yukihiko Yamashita and Toru Wakahara, “Affine-transformation and 2D-projection invariant k-NN classification of handwritten characters via a new matching measure,” Pattern Recognition, vol. 52, pp.459-470, April, 2016 DOI:10.1016/j.patcog.2015.10.002

- [4] Yoshikazu Washizawa, Tatsuya Yokota, and Yukihiko Yamashita, “Multiple kernel learning for quadratically constrained MAP classification,” IEICE Transactions on Information and Systems (letter), vol. E79-D, no. 5, pp.1340–1344, May, 2014. DOI:10.1587/transinf.E97.D.1340

- [5] Toru Wakahara and Yukihiko Yamashita, “k-NN classification of handwritten characters via accelerated GAT correlation,” Pattern Recognition vol. 47, no. 3, pp.994-1001, March, 2014. DOI:10.1016/j.patcog.2013.05.005

- [6] Joken Son, Naoya Inoue, and Yukihiko Yamashita, “Geometrically local isotropic independence and numerical analysis of the Mahalanobis metric in vector space,” Pattern Recognition Letters, vol. 31, issue 8, pp.709-716, June, 2010 DOI:10.1016/j.patrec.2009.07.018

- [7] Yukihiko Yamashita, “Optimum sampling vectors for Wiener filter noise reduction,”IEEE Trans. on Signal Processing, vol. 50, no. 1, pp.58-68, Jan., 2002. DOI:10.1109/78.972482

- [8] Toshihisa Tanaka and Yukihiko Yamashita, “Adaptive lapped transforms with overlapping basis functions for image coding,” J. Electronic Imaging, vol. 10, no. 3, pp.706-719, July, 2001. DOI:10.1117/1.1382613

- [9] Yukihiko Yamashita and Hidemitsu Ogawa, “Relative Karhunen-Loeve transform,”IEEE Trans. on Signal Processing, vol. 44, no. 2, pp.371-378, Feb., 1996 DOI:10.1109/78.485932

主な著作:
- [1] 山下幸彦, “線形システム論,”朝倉書店, 2013
- [2] 山下幸彦, 田中聡久, 鷲沢嘉一, “工学のための数学 工学のためのフーリエ解析,”数理工学社、2016.
教員からのメッセージ
- 山下幸彦 准教授より
ポリシーを持たないことが私のポリシーで、かなり柔軟な考えを持っているつもりです。自由な雰囲気の中で努力できる人が、今までの学問を踏み台にして、新たな学問を生み出すことができると思っています。
※この内容は掲載日時点の情報です。最新の研究内容については研究室サイト![]() をご覧ください。
をご覧ください。