物理学系 News&Information
竹内一将准教授が平成28年度東工大挑戦的研究賞を受賞
竹内一将准教授が、平成28年度東工大挑戦的研究賞を受賞しました。
挑戦的研究賞は、本学の若手教員の挑戦的研究の奨励を目的として、世界最先端の研究推進、未踏の分野の開拓、萌芽的研究の革新的展開又は解決が困難とされている重要課題の追求等に果敢に挑戦している独創性豊かな新進気鋭の研究者を表彰するとともに、研究費の支援を行うものです。本賞を受賞した研究者からは、数多くの文部科学大臣表彰受賞者が生まれています。
竹内一将 理学院 准教授
研究課題名:液晶乱流とホログラフィを用いた多体確率過程の普遍法則の実験検証

竹内一将准教授
私たちの周りは確率的な出来事であふれており、気流の乱れなどの自然現象から、交通流など人間活動に関するものまで、枚挙に暇がありません。確率的な事象がたくさん起こる場合、よく知られているのは統計学の中心極限定理であり、ガウス分布が普遍的に現れますが、これは事象間の相関が弱い場合にしか成り立ちません。では、多数の要素が強く相互作用する場合に現れる普遍的な法則はあるのでしょうか?
このような多体確率過程の解析は一般に極めて困難です。しかし、近年、Kardar-Parisi-Zhang(KPZ)クラスと呼ばれる、ある種の多体確率過程に関する数理的理解が急速に進展しており、そこではガウス分布と異なる分布関数が共通して現れると考えられています。もちろん、物理学としては、こうした普遍法則が自然界に実在するかが気になるところですが、我々は、液晶中で発生した乱流が成長する際の境界線の揺らぎがKPZ普遍法則に従うことを発見しています(図参照)。このように、揺らぎを伴う成長過程はKPZが期待される代表的な状況ですが、普遍的な分布関数の出現が定量的に確認されたのはこれが初めてでした。
中心極限定理と比べ、KPZが興味深いのは、実は初期状態によって幾つかの普遍法則に分類されるということです。現に我々の実験でも、初期状態が点か直線かで異なる分布関数が現れましたが、これらは様々な分類の一部に過ぎません。このたびご支援頂けることになりました研究課題では、液晶乱流の実験系にホログラフィ技術を組み合わせることで、乱流成長過程の初期状態を自在にデザインできるよう拡張し、KPZクラスのもつ様々な普遍法則の探求に挑戦しています。こうした研究を通して、強相関の多体確率過程の普遍性と多様性、またそのような普遍法則が自然現象に果たす役割まで、理解の深化に貢献していきたいと考えています。このたびは栄誉ある賞とご支援を賜り、どうもありがとうございました。
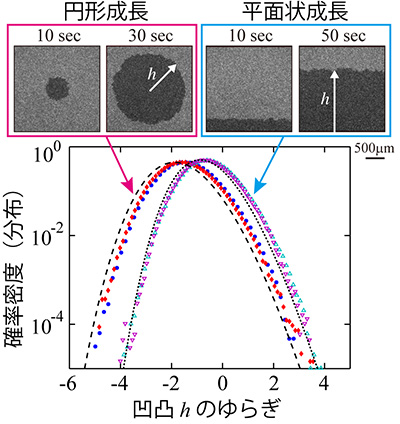
液晶乱流が成長する際の境界線の凹凸の揺らぎ。実験データ(色付き記号)とKPZの普遍的分布関数(破線・点線)と一致する。