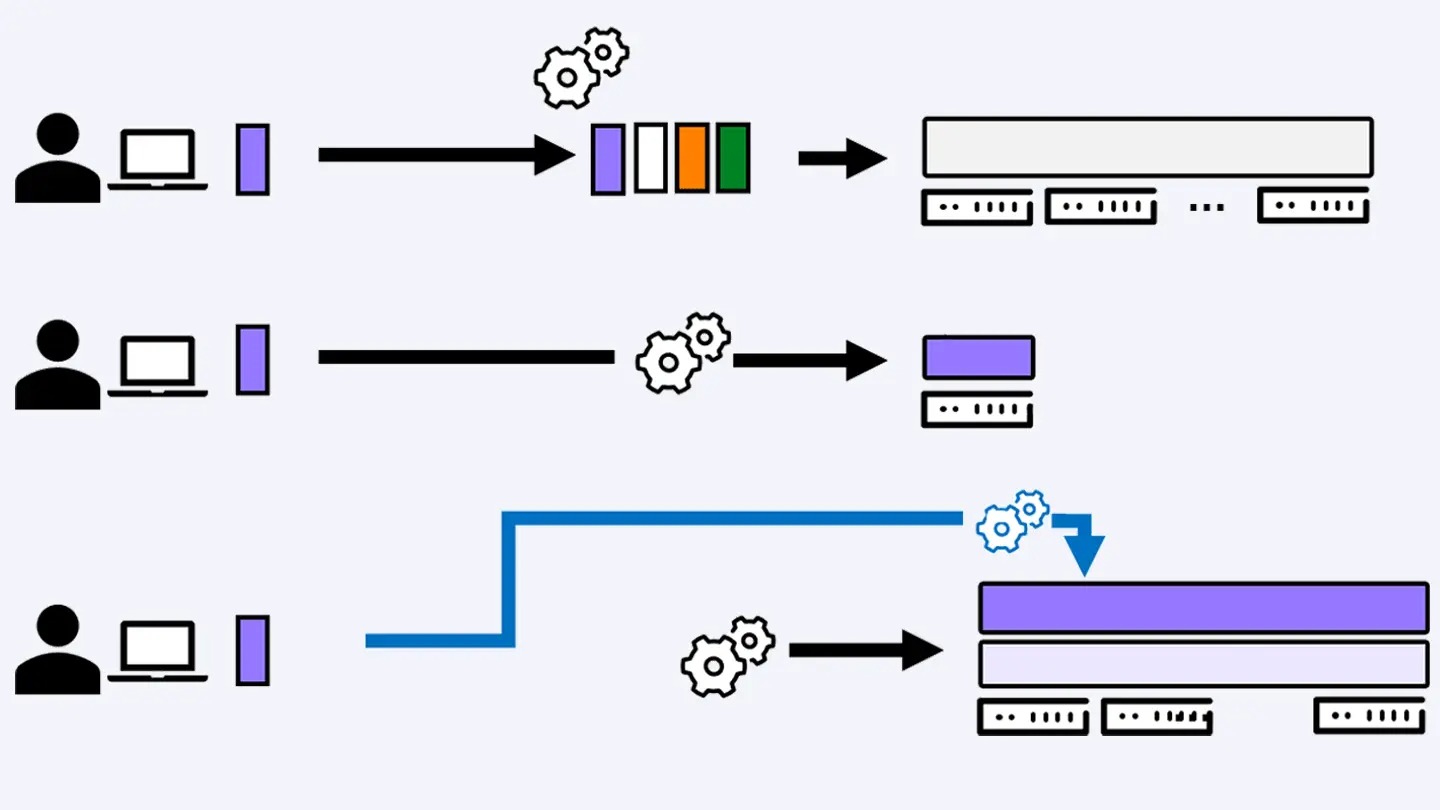
数理・計算科学系 News
新任教員の紹介 [数理流体力学, 微分方程式論]
この記事では2021年4月1日に数理・計算科学系に着任された後藤田剛助教にフォーカスします。
【研究内容】
私の研究テーマは流体運動を記述する微分方程式の数理解析です。特に、粘性流体の運動を記述するNavier-Stokes方程式や非粘性流体の運動を記述するEuler方程式、またそれらに関連する微分方程式を研究対象としています。微分方程式論ではどのような初期値や境界条件のもとで解が存在するのかはとても重要で基本的な問題です。一方で、現象を記述する数理モデルとして微分方程式を眺めると、解が時間発展した際にどのような振る舞いをするのかを知ることも現象の理解には大切です。私の研究テーマは、流体方程式について解の存在だけでなく具体的な解の挙動、特に渦運動に注目し、渦と渦の相互作用によってどのような現象が起きるのかを研究しています。実際の研究活動では数学解析だけでなく、数値計算も組み合わせることで流体現象の数理解析的な理解に取り組んでいます。
【最近の研究トピック】
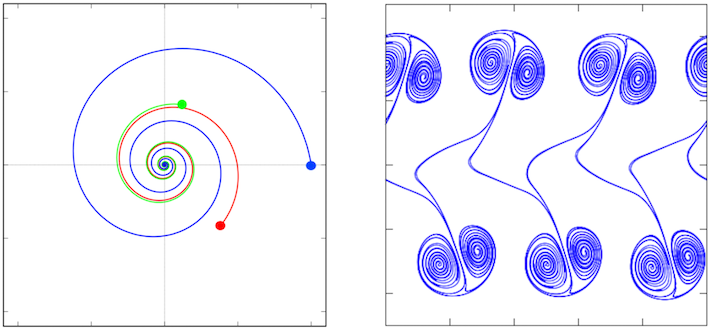
複雑な流体現象の理解には渦管、渦輪をはじめとする基本的な渦の相互作用を調べることが大切ですが、その数理解析にはしばしば困難が伴います。そこで、これらの渦に対してある種の数学的な理想化(単純化)を行うことで、渦の相互作用の本質的メカニズムを保持しつつ解析が比較的しやすい数理モデルが導出されます。例えば、二次元流体における渦斑や剪断層の渦領域は、渦度が局所領域に集中していると"理想化"することで、点渦や渦層と呼ばれる数学的に扱いやすい渦で記述できます。その非粘性流体における時間発展はEuler方程式から導かれる数理モデルによって記述することができ、実際に数学解析や数値計算を通して、点渦の自己相似衝突や渦層のパターン形成が起きることが知られています。最近の研究では、非粘性流体に対する数理モデリングや数学解析、数値計算などを通して、複雑な流体現象の素過程としての渦運動の理解に取り組んでいます。