新任教員の紹介 [可微分写像の特異点論]

この記事では2020年4月1日に数理・計算科学系に着任された一木俊助助教にフォーカスします。

【研究内容】
主に「可微分写像の特異点論」という数学の一分野を研究しています。本分野は、写像の特異点とよばれる点を調べる事で、写像や空間の性質を明らかにしていく分野になります。
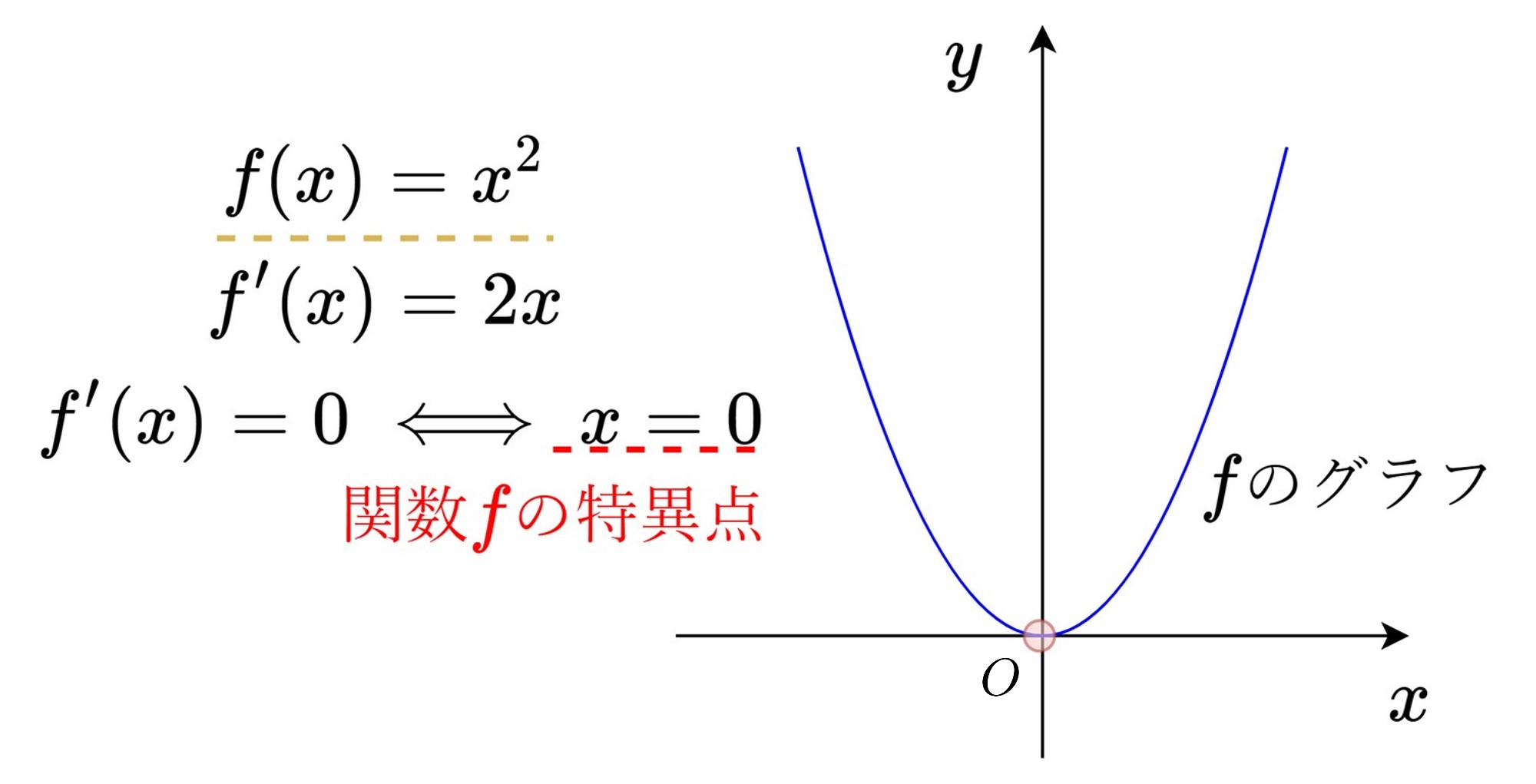
例えば、直線から直線への可微分関数のグラフの概形を調べる１つの方法として、まず関数を微分して０になる点を求めたと思いますが、まさにその点こそが、その関数の特異点になります。この事からも、関数のグラフを調べる際も、特異点を調べる事が重要な一つの鍵となっている事が分かります。

【最近の研究トピック】
「写像を集めた空間の中で、どのような性質をもつ写像が稠密に存在するのか」という事を事前に調べておけば、勝手に与えられた未知の写像でも、ちょっとだけ摂動する事で、その性質をもつ写像で近似できる事が数学的に保証できます。
最近私は、上述の「どのような性質をもつ写像が稠密に存在するのか」という事を調べる為の基本的道具（「横断性定理」とよばれる）の精密化や、新たな設定条件下における横断性定理を作ったりしています。
また、産業との親和性の高い多目的最適化理論にも興味を持っており、最近、特異点論の最適化への応用も得られました。今後も、自身の研究分野の他分野への応用も見つけていきたいと思います。

【担当授業】
「集合と位相第一演習」という大学２年生向けの演習の授業を担当しています。この授業では、集合論と位相空間論という分野の基本的概念を、演習問題を通して学んでいきます。今後数学を行っていく上で重要な、集合と写像という概念が度々登場するので、これらの扱いに慣れる絶好の機会となります。学生の皆様の力が付くような、良い演習問題と解説を用意していきたいと思っています。

【学生へのメッセージ】
疑問は、新しい課題発見に繋がる事もありますので、大切にする事をお勧めします。

• 一木俊助助教のresearch mapのページはこちら