情報通信系 News
都市の活性度を道路網の構造によって評価
要点
- 道路網情報から、都市の社会的、経済的活性度を表す中心地理論を開発
- 本理論を世界の92都市に適用し、その妥当性を検証
- 従来手法と比較し準備が容易であり、今後都市計画などへの適用が期待
概要
東京工業大学 科学技術創成研究院のペッター・ホルメ(Petter Holme)特任教授らは、都市と周辺の道路網の構造によって都市の活性度を評価する手法を開発した。幾何学的尺度Innessを定義し、出発点と目的地の最短と最速経路を評価・分析することで、都市とその周辺部の結合度を幾何学的分布で示した。さらに、この手法を世界の92の大都市とその周辺に適用し、都市の発展レベルを3種類に分類、社会経済的な相関を示すことに成功した。これにより、都市の活性度が道路網から容易に分かるようになった。都市とその周辺の活性度は普通、人口や物流、生産高などの社会的、経済的な指標に着目するのに対し、今回開発した手法はより簡便に把握することができる。
本研究成果は2017年12月20日、英国誌「Nature Communications」に掲載された。
研究の背景と経緯
今回の研究成果は中心地理論[用語1]に関するものである。これは、中心都市とその周辺地域の機能と規模を幾何学的な分布で示す地理学上の理論であり、1930年代にドイツの地理学者ヴァルター・クリスタラー(Walter Christaller)によって開発された。日本でも高度成長期には各地の都市計画などに利用された。これには、中心都市とその周辺地に関する多数の経済的、地理的データなどが必要だったが、これらの繁雑な準備が不要となる今回の研究成果は新しい中心地理論として注目される。
研究内容
幾何学的尺度 Inness の導入
都市中心地と周辺部の結合の強さを表現するため、幾何学的尺度Inness を定義した。図1-aで都市の中心地cから半径r(2、5、10、15、20、30 km)の距離にある円周に沿って36点を設け、この中から出発地Oと目的地Dを選ぶ。このODペアに対しインターネット上の地図情報(Open Source Map API[用語2])を参照し、生活道路などの最短経路(赤)と幹線道路などの最速経路(青)を選ぶ(図1-b)。ODペア(測地距離s)は都市中心から半径r、都市中心から見た出発地Oと目的地Dの間の角度をθとする。図1-cで示すように、(赤の内点と直線の測地線[用語3]で区切られたポリゴン[用語4])から(青の外点と測地線で区切られたポリゴン)の差を Inness と定義する。Innessが正の場合はODペアの測地線より経路が内側にあり、負の場合は外側にある。ODペアの経路と測地線の関係から、図1-dに示すようにポリゴンの形状は3つのケースがある。Innessが正であれば赤で塗られた領域が広く、負であれば青で塗られた領域が広くなる。
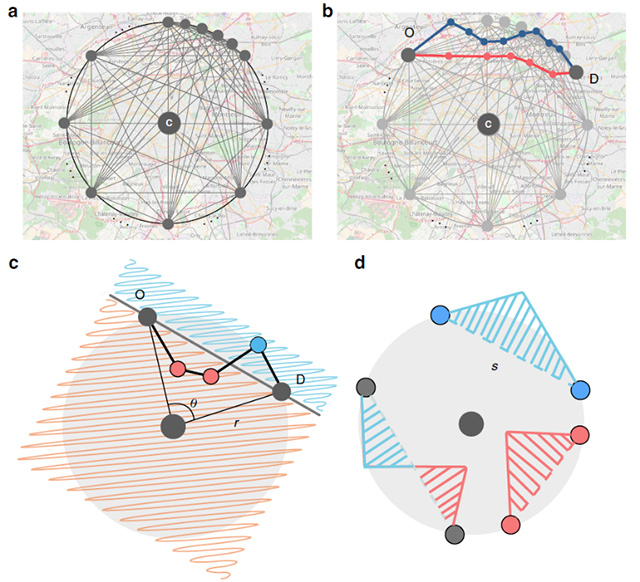
図1. Innessの定義
Innessの意味
図2は世界の92都市について、平均的なInnessを示したものである。最短/最速経路について都市中心から見込む角度θについて、Innessの平均値と標準偏差を示す。都市中心地付近(r=2 km)ではInnessはほぼ0であり、これは経路が市中の生活道路であるためと推定される。一方、郊外になると(r=10、30 km)、Innessの変動も大きくなる。これは、中心地に向かう幹線道路や環状道路、バイパス道路などの影響と思われる。
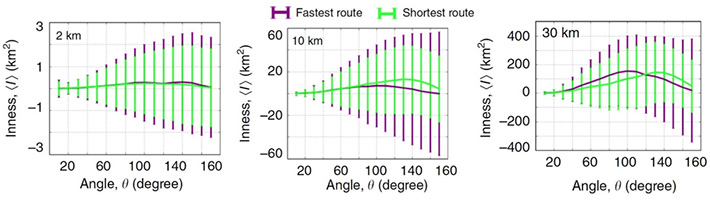
図2. 都市中心地からのr、θを関数とするInnessの平均値と標準偏差
このようにして得られたInnessは靴紐のアルゴリズム[用語5]によって、地図上にポリゴンの集合として配置される。
世界の主要都市を分類
それではInnessを用いて、世界の92都市の分類してみよう。都市の面積は様々なため正規化[用語6]し、Innessの平均値と標準偏差値をプロットすると、3つのグループに分類できた(図3)。2つの値がともに低いLLグループにはベルリン、パリ、東京などの大都市が入る。道路の全長が長く、地理的制約が少なく、周辺との接続性もよく、インフラ整備も進んでいる。図3左中のベルリンでは、Innessが正の領域が偏りなく広がり、うすい赤で表示されている。これから分かるように都市機能は分散し、中心地と見なされる点は見当たらない。一方、平均値と標準偏差値がともに高いHHグループは、図3右のカルカッタを例にすると、中心部のInnessは正でしかも濃い赤の領域が広がっている。これは、道路のインフラ整備が不充分で、周辺部との接続性が限定され、主要な交通経路は都市の中心地を経由することになり、中心地の混雑が予想される。また、平均値が低く標準偏差の高いLHグループは、LLとHHグループの中間的性格も含むが、地理的制約による要因も無視できない。例えば、図3中のムンバイは大陸に隣接した島にあり、中心部はInnessが適度な正でうすい赤の領域が広がっているが、周辺部とは橋で接続されるため遠回りせねばならず、Innessは負で青い領域が広がっている。
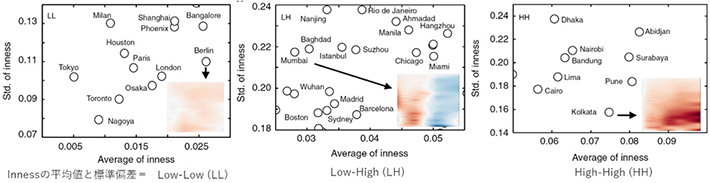
図3. 世界の都市のInnessの統計と分布
Innessと社会経済的関連性
次に、各都市の最短経路と最速経路について分析した。前者は地理的制約によるが、後者は環状線や高速道路などの社会的発展指標と関連している。ある都市の正規化した最短経路のInnessと最速経路のInnessのピアソン相関係数ρ[用語7]を求めた。道路網が未整備だと、最短経路と最速経路は大差ない経路となり、両者は正の相関がありρは1に近づく。一方、自動車幹線道路が整備されると最短経路と最速経路は別ルートとなり、両者の相関関係は小さくなりρは0に近づく。その値を昇順に並べたものが図4のRank of citiesである。
これらのデータをk平均法[用語8]や自然分類法[用語9]によりTYPE I、TYPE II、TYPE IIIに分類すると、TYPE IはグループLL、TYPE IIはグループLH、TYPE IIIはグループHHにほぼ対応している。そして図4右に、相関係数ρと1人当たりGDPの関係を示したように、これらの間には明確な相関があることが分かった。このことから、Innessは都市の地理的な評価のみならず、社会経済的な指標にもなり得ることが確かめられた。
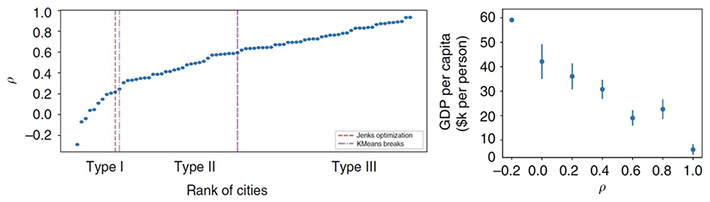
図4. 都市の最短経路と最速経路による分析、及びGDPとの関係
今後の展望
本方式で中心地理論を展開するには、基本的にはインターネット上の最新の地図情報(Open Street Map database)があればよい。従来は地図情報に加えて、社会経済的指標を示すデータ(例えば、地域内の学校数、工場数、余裕電話台数など)が必要であり、これらは時代とともに変化するため、その設定は容易でなかった。本方式は、現状の都市周辺の活性度を評価するだけでなく、将来の道路網整備が地域全体に与える効果を予測する手段となる可能性がある。
本研究の一部は、東京工業大学が展開しているワールド・リサーチ・ハブ・イニシアティブ(WRHI)によって行われた。WRHIは「世界の研究ハブ」を目指す組織として、世界トップレベルの研究者を招へいし、国際共同研究の加速と分野を超えた交流を実施している。
用語説明
都市をある地域の中心地という観点から把握した、都市の分布、数、規模 (大きさ) などの規則性に関する理論。中心地には、都市の機能によって高次から低次への階層性があり、その機能の及ぶ範囲を都市圏と呼ぶ。また機能の大きさ、度合いを中心性と呼んでいる。
曲面上で二点間を結ぶ曲線のうち最短距離のもの。球面上では大円の弧。
多角形。三次元のコンピューターグラフィックスにおける立体形状を表現するために使われる多角形を指すことが多い。物体表面を小さい多角形(主に三角形)に分割し、その位置や角度、模様、質感などの見え方を個々に計算して三次元画像を描画する。
[用語5] 靴紐のアルゴリズム(shoelace formula for polygons)
ガウスの面積公式とも呼ばれる。平面において多角形の頂点座標によってその面積を求める数学的アルゴリズム。座標値を直接用いた四則演算のみで面積が求められるため、計算機上での求積に適しており、また余計な誤差が入り込む余地が少ない。
一定の規則に従い、データを変形し利用しやすくすること。リレーショナルデータベースの設計でよく用いられる。
[用語7] ピアソン相関係数ρ(Pearson's correlation coefficient ρ)
2つの確率変数の間にある線形な関係の強弱を測る指標。相関係数が正のとき確率変数には正の相関が、負のとき確率変数には負の相関があり、0の場合は相関はない。
[用語8] k平均法(k-means clustering)
非階層型クラスタリングのアルゴリズム。クラスタの平均を用い、与えられたクラスタ数k個に分類する。
データの変化量が比較的大きいところに閾値が設定される分類方法。
論文情報
| 掲載誌 : | NATURE COMMUNICATIONS | 8: 2229 |
|---|---|
| 論文タイトル : | Morphology of travel routes and the organization of cities |
| 著者 : | Minjin Lee, Hugo Barbosa, Hyejin Youn, Petter Holme, Gourab Ghoshal |
| DOI : | 10.1038/s41467-017-02374-7 |
- 研究者詳細情報(STAR Search) - ホルメ ペッター Petter Holme
- 東京工業大学 科学技術創成研究院 (IIR)
- WRHI - Tokyo Tech World Research Hub Initiative
- 研究成果一覧