経営工学系 News
繰り返しオークションの統一的解析手法を考案
離散最適化分野の理論を駆使
概要
東京工業大学工学院経営工学系の塩浦昭義准教授らは、住宅や自動車、さらには空港の発着枠や電波の周波数のような複数の「商品」を扱う繰り返しオークションに対する統一的な解析手法の考案に成功した。離散最適化分野[用語1]における離散凸解析と呼ばれる理論を用いて実現した。
これにより、オークションの異なるモデルに対して独立に提案されていた様々な繰り返しオークションを統一的な視点から理解することができるようになった。さらに、既存の繰り返しオークションをより複雑なモデルに拡張するとともに、離散凸解析における研究成果を生かして、新たな繰り返しオークションを提案した。
研究の背景
オークションの目的はオークションにかけられた商品の勝者を決めることと同時に、商品の「適正な」価格(均衡価格とよばれる)を決めることである。商品の均衡価格の計算には、入札者の希望を聞きながら価格を徐々に修正していく、繰り返しオークションと呼ばれるアルゴリズム(計算方法)がしばしば用いられる。
扱う商品が1つの場合、価格を徐々に上げていき、オークションの勝者と均衡価格を決めるイングリッシュ・オークションがよく用いられる。これは繰り返しオークションの典型例である。
商品の数が1つの場合、繰り返しオークションの解析は比較的容易である。しかし、商品数が複数の場合には各商品に対する入札者の希望が複雑に絡み合うため、繰り返しオークションの解析は困難であり、アルゴリズムの振る舞いは理論的に十分に理解できているとは言いがたい状況であった。
また様々なオークションのモデル(入札者が入手できる商品数が1つか複数か、あるいは各商品の在庫が1つか複数かなど)に応じて様々な繰り返しオークションが提案されている。しかし、それらの関係については明らかにされていない部分が多かった。
一方、離散最適化問題の中には短い計算時間で解ける「易しい」問題もあれば、何時間を費やしてもなかなか解けない「難しい」問題もある。解きやすい離散最適化問題に共通する「良い」数学的な性質を「離散凸性」という視点から明らかにしようという理論が離散凸解析である。離散凸性をもつ問題に対しては局所的最小性が大域的最小性を導くとともに、ある種の双対定理が成り立つので、最適解を見つけやすくなる。
例えば、カーナビなどで使われる、ある地点から目的地への最短経路を求めるという問題(最短経路問題)は「易しい」問題である。これに対し、宅配便による荷物の配送のように、決められた複数の地点を最短距離で巡回する経路を求める問題(最短巡回路問題)は「難しい」問題である。これらは離散凸性と密接な関係があり、前者の最短経路問題は離散凸性をもつので解きやすく、後者の最短巡回路問題は離散凸性をもたないので解きにくいと理解することができる。
研究成果
塩浦准教授らは、商品の均衡価格を計算するという問題が、ある種の離散最適化問題として表現できるという事実を鍵として用いた。この離散最適化問題が離散凸性という数学的に「良い」性質をもつことを明らかにした。
これにより、均衡価格の計算が数学的な観点からみて「良い」構造をもつ問題であることがわかった。また均衡価格の計算に用いられる繰り返しオークションのアルゴリズムの理論的な解析において、離散凸解析の理論における過去の研究成果が適用できることもわかった。
その結果、オークションの異なるモデルに対して独立に提案されていた様々な繰り返しオークションを統一的な視点から理解することができるようになった。さらに、既存の繰り返しオークションをより複雑なモデルに拡張するとともに、離散凸解析における研究成果を生かし、新たな繰り返しオークションを提案した。
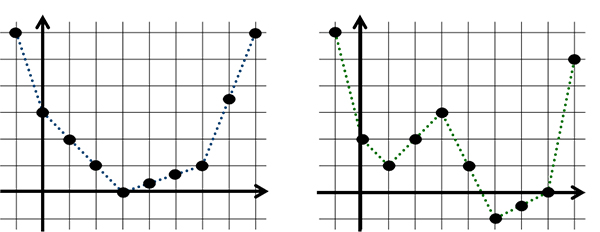
図1.離散凸性のイメージ図
左は離散凸性をもつ関数、右は離散凸性をもたない関数の例である。離散凸性をもつ関数の場合、極小な点は必ず最小になるが、離散凸性をもたない関数の場合は極小であっても最小である保証はない。
用語説明
[用語1] 離散最適化 : 最適化問題とはいくつかの選択肢の集合(解集合)の中から、ある評価尺度(総コスト、総時間、総距離など解に関する関数として表現される)の下で、最も良いもの(最適解)を求めよ、という問題である。最適化問題は解集合の種類によって大きく二分され、液体の量や土地の面積のように解を実数値で表すことができ、連続的に変化できる場合と、解集合がバラバラなものの集まりであって、解を連続的に変化させることができない(離散的な)場合がある。離散的な解集合の典型的な例としては、欲しい商品の組合せや交通ネットワークにおける経路などが挙げられる。離散的な解集合に関する最適化問題のことを離散最適化問題という。離散最適化問題を数学的な視点から解析し、高速・高性能な解法の構築を目指す研究分野が離散最適化である。
論文情報
掲載誌 : |
Discrete Optimization, 19, pp.36-62, (2016) |
論文タイトル : |
Time Bounds for Iterative Auctions: A Unified Approach by Discrete Convex Analysis |
著者 : |
Kazuo Murota1, Akiyoshi Shioura2, Zaifu Yang3 |
DOI : |
|
所属 : |
1School of Business Administration, Tokyo Metropolitan University,
2Department of Social Engineering, Tokyo Institute of Technology,
3Department of Economics, University of York |
問い合わせ先
工学院経営工学系
准教授 塩浦昭義
Email : shioura.a.aa@m.titech.ac.jp



