Electrical and Electronic Engineering News
Finding Order Using Chaos: Synchronization of Spiking Oscillators Helps Build Physical Reservoirs
Engineers at the Tokyo Institute of Technology (Tokyo Tech) have demonstrated a computational approach using a ring network of coupled spiking oscillators with chaotic dynamics implemented on analog hardware. This new approach is based on the emergence and pattern formation phenomena that occur under "incomplete synchronization" within chaotic dynamics. In the future, it could significantly impact conventional methods for pattern detection commonly used in artificial neural networks on digital hardware counterparts.
In recent times, algorithms based on artificial intelligence (AI) are finding various societal applications such as personalized healthcare, autonomous driving, smart cities and precision farming. The amount of computing capability necessary to deploy such algorithms is increasing. Therefore, research initiatives are looking at alternative AI approaches taking inspiration from existing natural systems.
One approach is physical reservoir computing, where an ensemble of dynamical elements exploiting physical phenomena is used to map input data onto a high-dimensional space. The merit of this method is the reduced need for training algorithms that require a large amount of processing power. These reservoirs can often be implemented by very simple physical systems and do not require complex architectures as is the case with neural networks. The circuit that was used in this study, named the Minati-Frasca circuit and initially discovered and developed by researchers at the Universities of Trento and Catania in Italy, is highly elementary, involving only five passive and two active components, while showing rich spiking behavior[1]. "These circuits are truly remarkable and are a natural candidate for physical reservoir computing," says Dr. Hiroyuki Ito, head of the Nano Sensing Unit where the study was conducted.
The experiments performed by the researchers at Tokyo Tech included tuning the chaoticity and coupling strength within a ring network of Minati-Frasca circuits (Fig. 1a). Initially, at low values of a suitable control parameter, the network showed periodic spiking, followed by highly irregular behavior when this parameter was increased (Fig. 1b, left). In combination with sweeping the coupling strength, this operation revealed a rich variety of ways in which the network synchronizes, meaning that nodes within it show similar behavior as can be observed in their waveforms (Fig. 1b, right). Considering the network as a whole, the emergence of synchronization patterns with a preferential synchronization of some node pairs over others, a situation known as incomplete synchronization, can be observed within chaos (Fig. 1c). Furthermore, in the case of this particular network, this region reaches maximal width near the edge of chaos, which is the boundary between periodic and chaotic regions of operation.
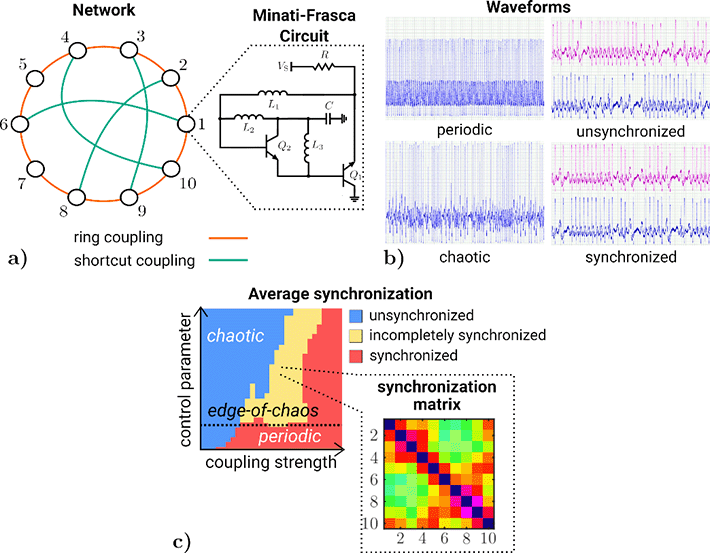
Figure 1. Overview of the network of chaotic oscillators, their generated waveforms and synchronization behaviors.
- Image caption: a) Topology of the network and node circuit diagram, b) Waveforms of a single node operating in periodic (top-left) and chaotic regions (bottom-left) followed by waveforms of two coupled nodes that are unsynchronized (top-right) and synchronized (bottom-right). c) Average synchronization across the entire network under the control of the coupling strength and a parameter that influences the dynamics of the circuit. The regions where the network is unsynchronized (blue), incompletely synchronized (yellow) and completely synchronized (red) are shown. A broad region of incomplete synchronization, when the network is operating near the edge of chaos, can be observed. Furthermore, the synchronization matrix in the region of incomplete synchronization shows the emergence of preferential entrainment between some node pairs with respect to others. Image credit: Jim Bartels.
The researchers at Tokyo Tech then introduced two additional factors to influence the "route-to-synchronization," namely, the injection of coherent noise into each node within the network (Fig. 2a, left) and splitting of the network into two different populations (Fig. 2b). The former showed that the extra noise significantly reduces the synchronization of the network in the periodic region, while, in the chaotic region, the area of incomplete synchronization (Fig. 2a, right) shifts and the synchronization of nodes that are not structurally adjacent is enhanced. This indicates that the network can respond to external stimuli in a complex manner. The latter experiment split the network into two halves, one operating within chaos (A) and the other within periodicity (B). The route-to-synchronization under this condition was examined with a coupling strength sweep, producing a striking diversification of the synchronization behaviors between the two populations. While the synchronization strength steadily increased within the chaotic half, the periodic half showed non-monotonic effects, i.e., multiple minima appeared when sweeping the coupling strength (Fig. 2b right). In addition, upon investigating the synchronization patterns in detail, an adversarial behavior was revealed, showing an initial synchronization of the periodic half which was then overtaken by the chaotic half, followed by a final overall synchronization between both halves. This effect further underlines the generative potential of this network. In essence, a binary split of two populations shows a highly simplified scenario of the input perturbations that this network could be exposed to when used for physical reservoir computing.
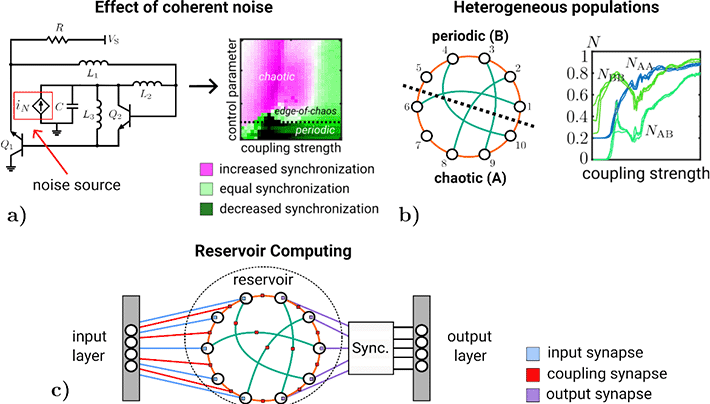
Figure 2. Effect of coherent noise and heterogeneous populations on the synchronization phenomena of the network and proposed physical reservoir.
- a) Effect of coherent noise injected into the network, realized by means of an additional current source. The parameter map shows the difference in average synchronization between no noise and maximal induced noise. b) Splitting the network into two halves, one operating in chaos (A) and the other showing periodic behavior (B), by setting the control parameter differently. Non-monotonic effects are observed from the plot for the periodic half, revealing adversarial road-to-synchronization effects across nodes. c) Hypothetical configuration of the network of chaotic oscillators when used as a reservoir, receiving perturbations on the coupling strengths and the control parameter. Image credit: Jim Bartels.
As such, the researchers considered the network in their study and proposed to use it for implementing reservoir computing in the future by exploiting the various phenomena that were described above (Fig. 2c). "Coming from a background of machine learning, the couplings within the network reminded me of working with neural networks. However, at first I was not able to understand the implications of changing dynamics and chaos, since conventional AI algorithms tend not to have their innate dynamical activity," says Jim Bartels, one of the lead authors of this study. "I realized that exploiting these dynamics for computation could fit well into the field of reservoir computing, which remains a growing area of study."
After this interview, the team explained why this type of reservoir computing could be beneficial for applications in society. "One of the main fields of research that we are working on in the Nano Sensing Unit is time series classification for internet-of-things (IoT) devices and edge computing, such as animal behavior classification [2]. A very important consideration for these devices is their battery lifetime, since it determines the barrier towards concrete adoption. What is exciting about physical reservoirs such as the one we have proposed is the possibility of operating, in future integrated realizations yet to be built, at a lower power than large digital neural networks. As the circuit represents one of the smallest known types of spike-generating oscillators, going beyond the present proof-of-concept stage, we expect researchers worldwide to explore its many possible variations for additional computational frameworks, such as neural networks," commented Dr. hab. Eur-Ing. Ludovico Minati, who is the leading author of the study. The experiments that were undertaken, the design of the hardware, the results and their discussion are reported in a recent article published in the journal Chaos, Solitons & Fractals [3]. Furthermore, all design materials and experimental data have been made freely downloadable.
- References
[1] Sprott JC, Thio WJC, Elegant Circuits: Simple Chaotic Oscillators, Singapore: World Scientific 2022, DOI: 10.1142/12362![]()
[2] Bartels J, Tokgoz KK, A S, Fukawa M, Otsubo S, Li C, Takeda K Rachi I, Minati L, Ito H, TinyCowNet: Memory- and Power-Minimized RNNs Implementable on Tiny Edge Devices for Lifelong Cow Behavior Distribution Estimation, IEEE Access, vol. 10, pp. 32706-32727, 2022, DOI: 10.1109/ACCESS.2022.3156278![]()
[3] Minati L, Bartels J, Li C, Frasca M, Ito H, Synchronization phenomena in dual-transistor spiking oscillators realized experimentally towards physical reservoirs, Chaos, Solitons and Fractals, vol. 162, art. 112415, 2022, DOI: 10.1016/j.chaos.2022.112415![]()
- Reference
| Authors : | Ludovico Minati1,2, Jim Bartels1, Chao Li1, Mattia Frasca3,4, Hiroyuki Ito1 |
|---|---|
| Title of original paper : | Synchronization phenomena in dual-transistor spiking oscillators realized experimentally towards physical reservoirs |
| Journal : | Chaos, Solitons & Fractals |
| DOI : | 10.1016/j.chaos.2022.112415 |
| Affiliations : | 1 Nano Sensing Unit, Institute of Innovative Research, Tokyo Institute of Technology, 226-8503 Yokohama, Japan 2 Center for Mind/Brain Science (CIMeC), University of Trento, 38123 Trento, Italy 3 Department of Electrical Electronic and Computer Engineering, University of Catania, 95131 Catania, Italy 4 "A. Ruberti" Institute for Systems Analysis and Computer Science, National Research Council (IASI-CNR), Rome 00185, Italy |
- Just Listen to the Chaos: A New Approach to Extracting Information from Large Ensembles of Sensors | Tokyo Tech News
- Many Buds to a Blossom: a Synchronization Approach to Sensing Using Many Oscillators to Make a Measurement | Tokyo Tech News
- Nonlinear fureai: How connectedness can nurture complex dynamics across diverse networks | Tokyo Tech News
- A simple, yet versatile, new design for chaotic oscillating circuitry inspired by prime numbers | Tokyo Tech News
- Using Edge AI to listen to the "silent voices" of cattle | Tokyo Tech News
- Mathematical monotsukuri: Summing a constant may help to detect synchronized brain activity | Tokyo Tech News
- Tokyo Tech's six-legged robots get closer to nature | Tokyo Tech News
- Ludovico Minati | WRHI - Tokyo Tech World Research Hub Initiative
- Ito Laboratory
- Ludovico Minati | Researcher Finder - Tokyo Tech STAR Search
- Hiroyuki Ito | Researcher Finder - Tokyo Tech STAR Search
- Institute of Innovative Research (IIR)
- Laboratory for Future Interdisciplinary Research of Science and Technology (FIRST)
- Electrical and Electronic Engineering Graduate Major|Eduaction|Department of Electrical and Electronic Engineering, School of Engineering
- Electrical and Electronic Engineering Undergraduate Major|Eduaction|Department of Electrical and Electronic Engineering, School of Engineering
- Latest Research News
Further Information
Associate Professor Ludovico Minati
Institute of Innovative Research, Tokyo Institute of Technology