Professor Isao Yamada received Prizes for Science and Technology in 2016 MEXT Commendation

Isao Yamada
Professor, School of Engineering / Director, Global Scientific Information and Computing Center

Prize-winning research: Signal processing based on the fixed-point expression of a nonexpansive mapping

Prof. Yamada

Developing alongside mathematics, signal processing has kept on evolving since the time of Euclid as a fundamental technique for estimating valuable information from observed data. It has been applied to a broad range of measurement and information technology systems. The majority of present-day signal processing technology applies the strategies of least-squares estimation by Gauss and orthogonal function expansion by Fourier, and is commonly based on information expression in terms of subspaces (in the sense of linear algebra) and the orthogonal projection theorem (Pythagorean theorem generalized in Hilbert space). A key to dramatic progress in signal processing must be synergetic effects generated through certain nontrivial integrations of the powerful ideas for set expression and for optimization in modern computational mathematics.

Thanks to spectacular progress in the theory of convex analysis, a variety of information that was not applicable efficiently to signal processing and inverse problems has been revealed to have precise expression as the fixed point set of certain nonexpansive mappings (Fig.1 and 2).

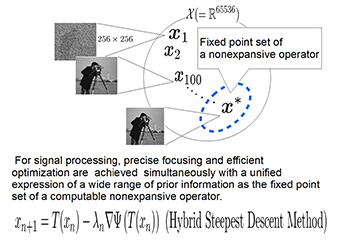
Fig. 1 A conceptual diagram processing based on the fixed-point expression of a nonexpansive mapping

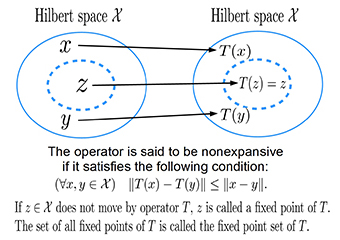
Fig. 2 The nonexpansive mapping and fixed point set utilized in this study

The hybrid steepest descent method in this study was developed by a nontrivial integration of the fixed point theorem and convex optimization, and the world's first algorithm that succeeded in solving generic convex optimization problems defined over the fixed point set of a nonexpansive mapping (Fig. 1). Boldly relaxing this idea, we also developed the adaptive projected subgradient method and successfully solved the problem of asymptotic minimization of sequence of convex functions. These are the central algorithms for applying fully the outstanding ideas in the fixed-point expression of a nonexpansive mapping to signal processing. They have exhibited excellent performance in application to a number of inverse, adaptive signal processing, and online machine learning problems.

It is an honor to have research I have been involved in for so long regarded highly by MEXT. I would like to express my deep appreciation to my students and research partners for their dedication and cooperation. The true value of this study will be tested from now, but I believe that we have reached the starting point for further development. I would like to continue with this research to achieve further results in the field of signal processing, optimization, and inverse problems.