Symmetry is essential for power network synchronization

Graph theory contributes to stable power supply under the large and complex electric power system

May 15, 2018

A joint research team from Tokyo Tech and North Carolina State University has clarified the fundamental principles for achieving the synchronization of power generator groups¹ in power networks, which is essential for the stable supply of electric power. Based on this principle, the team developed a method for constructing an aggregated model of a power network that can efficiently analyze and control the behavior of generator groups (including rotor phase angles and connection point voltages) with complex connection to a power grid.

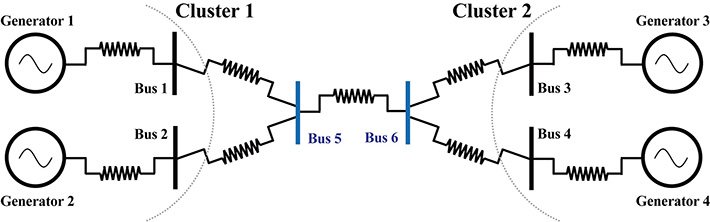
Example of a symmetrical power network for a bus (connection point)

Figure 1. Example of a symmetrical power network for a bus (connection point)

A power network consisting of four generators and six buses (connection points). Generators 1 and 2 and Buses 1 and 2 to which these are connected become a symmetrical network for Bus 5. Similarly, Generators 3 and 4 and Buses 3 and 4 become symmetrical for Bus 6. The two sets of symmetrical generator groups and buses are shown as Clusters 1 and 2.

Background

It is known that the synchronization phenomenon of generator groups such as at multiple thermal power plants is closely related to the stable supply of electric power. Specifically, if a generator becomes out of synchronization, that generator and its surrounding generators will not be able to operate stably, and in worst cases, serious accidents such as power outages can occur.

In addition, energy problems caused by global warming and the depletion of fossil fuels have become more serious on a global scale. Therefore, from the viewpoint of reducing carbon dioxide and systematic use of energy, high expectations have been placed on renewable energy such as typified by photovoltaic (PV) generation. When large-scale PV generation equipment and power storage equipment are introduced, in addition to power generation such as thermal power, hydraulic power, and nuclear power that are commonly used today, it is necessary to consider power charge and discharge by PV generated output and storage batteries in order to maintain equilibrium between supply and demand. However, the amount of power from PV generation fluctuates since there is uncertainty related to changes in weather and changes in solar radiation volume according to the time zone. This makes it more difficult to maintain the synchronization of generator groups. The need to analyze synchronization is greater than ever.

With conventional analysis, a major approach is based on numerical simulation. There are no studies that theoretically clarify the basic principles for how to properly synchronize generator groups according to the network structure of power transmission. There is an urgent need to build a power supply and demand framework that efficiently utilizes power storage equipment to allow for the uncertainty of PV generation and demand predictions.

Overview of Research Achievement

Assistant Professor Takayuki Ishizaki, Professor Jun-ichi Imura of Tokyo Tech, and Associate Professor Aranya Chakrabortty of the NSF ERC FREEDM System Center at North Carolina State University worked on multiple studies including power network modeling, stability analysis, and stabilization control from the perspective of graph theory². They have clarified that the symmetry of the network in graph theory is the fundamental principle for realizing the synchronization of generator groups at thermal power plants integrated with power grids (connected to a network).

The behavior of generators connected through a network in a power grid is represented by complex equations (differential algebraic equations) that combine differential equations and algebraic equations. The differential equations express "behavior of generators" derived from Newton's second law of motion, and the algebraic equations express "power balance at power grid connection points" derived from Ohm's law and Kirchhoff's law³ . Analysis of these differential algebraic equations was generally performed by transformation into a mathematically equivalent differential equation through a simplification method called the Kron reduction. However, the problems were that with the existing approach, since the algebraic equation representing the power grid is eliminated by deleting the redundant variable representing the connection point voltage, it was not very suitable for analyzing the relationship between the network structure of the power grid and the behavior of the generator.

To resolve this issue, they analyzed the network structure of the power grid contained in the algebraic equations from the viewpoint of symmetry based on an understanding of graph theory. Specifically, by analyzing the behavior of the generator without eliminating the algebraic equations, they discovered that the symmetry of the power grid (Figure 1) is the basic principle for realizing synchronization of generator groups. In addition, based on a new idea of simultaneously integrating generator groups that show synchronous behavior and the power grid that couples these, it became possible to mathematically and physically construct a feasible aggregated model (Figure 2).

It is expected that this achievement will result in a basis for developing analysis and control methods for realizing stable power supply to large and complex electric power systems. In the future, Professor Imura says that it aims to develop more complex electric power systems including converters, and to establish a theory to approximate the synchronization of generator groups.

This research result was published in "Proceedings of the IEEE" on April 25, 2018.

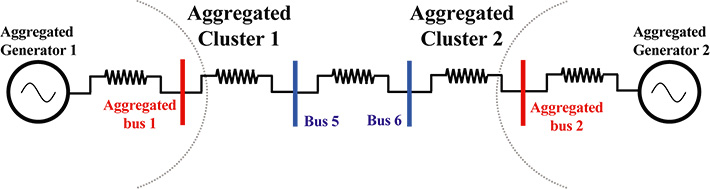
Integrated power network

Figure 2. Integrated power network

Synchronized cluster of an aggregated model obtained by simultaneously integrating the two sets of symmetrical generator groups and buss (connection point) groups in Figure 1. According to Ohm's law and Kirchhoff's law, it is a mathematically and physically feasible aggregated model.

1 Synchronization of Generator Groups

The phase angles of the rotors such as the turbines of multiple generators must be the same or reasonably close. Each rotor rotates according to the standard of a specific frequency (50 Hz or 60 Hz in Japan) in order to maintain its frequency. A difference in the frequency of each generator creates a difference in phase angle.

2 Graph Theory

This is a mathematical theory related to graphs (network structure) composed of sets of vertices (nodes) and sets of edges. The power grid network is interpreted as a graph in which the connection point is the vertex and the transmission line linking the connection points is the edge.

3 Ohm's Law, Kirchhoff's Law

These are physical laws that express the relationship between physical quantities such as voltage and current in an electric circuit. Ohm's law indicates that the voltage difference between two points in a circuit is proportional to the current flowing between them. Kirchhoff's law indicates that at the branch point in the circuit, the sum of the currents flowing to that point is equal to the sum of the currents flowing from that point.

Reference

Authors :	Takayuki Ishizaki¹, Aranya Chakrabortty², Jun-ichi Imura^1*
Title of original paper :	Graph-Theoretic Analysis of Power Systems
Journal :	Proceedings of the IEEE
DOI :	10.1109/JPROC.2018.2812298
Affiliations :	¹Graduate School of Information Science and Engineering, Tokyo Institute of Technology ²Electrical & Computer Engineering, North Carolina State University