Research Laboratories
and Subjects

• Honda Lab
  

  Exploring new spaces

  We explore the geometry of spaces which naturally arise from differential geometry.
  • Complex geometry
  Detailed Site
• Oya Laboratory
  

  Representation theory and its application

  We study representations of algebraic objects appearing in Lie theory. We also investigate some geometric objects in terms of representation theory.
  • Representation theory
  • Kac-Moody Lie algebras
  • Quantum groups
  • Cluster algebras
  Detailed Site
• Ochiai Laboratory
  

  Towards broader and deeper understanding of Number theory

  We study zeta functions and L-functions in Number theory using various tools from Galois representations, automorphic representations and algebraic geometry.
  • Iwasawa theory
  • Hida theory
  • Zeta functions and L-functions
  Detailed Site
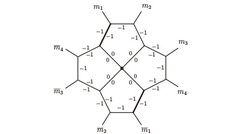
• Purkait Laboratory

  

  Discovering "New" operators

  We study local Hecke algebras of the covering groups and characterisation of the newspace of half-integral weight modular forms.

  • Number theory
  • Modular forms
  • Automorphic representations
• Shinya Nishibata Research Group

  

  Differential equations in mathematical physics

  • Mathematics
  • Analysis
  • Theory of differential equations
  • Mathematical physics
• Tonegawa Lab
  

  Analyzing geometric problems using analysis

  We carry out research projects related to minimal surface theory, one of the most important research fields in the calculus of variations.
  • Minimal surface
  • Flow problems
  • Geometric analysis
  • Differential equations
  Detailed Site
• Taguchi Laboratory

  

  Enjoy number theory!

  We study Galois representations of global/local fields, and their moduli spaces.

  • Number theory
  • Number field, function field
  • Galois representation
  • Moduli space
• Suzuki Laboratory
  

  No royal road to number theory

  We work on the study of numbers using mainly analytic techniques.
  • Analytic number theory
  Detailed Site
• Gomi Laboratory

  

  Topology and Physics

  I study themes in algebraic topology related to physics.

  • algebraic topology
• Masaaki Umehara Research Group

  

  Visual curves and surfaces

  Working on differential geometry, we are interested in maximal surfaces in Lorentzian 3-space and isometric deformations of singularities.

  • Differential geometry
  • Manifolds
  • Curves and surfaces
• Yatagawa Laboratory

  

  Ramification theory and some invariants

  We study ralations between some invariants in algebraic geometry and invariants in ramification theory in algebraic number theory.

  • Algebraic number theory
  • Etale cohomology
  • Ramification theory
• Sakie Suzuki research group
  

  Knot theory and Quantum topology

  I am studying quantum invariants of knots and 3 dimensional manifolds. I enjoy watching the world where geometric intuition and algebraic theory coexist exquisitely.
  • Knot theory
  • Quantum topology
  Detailed Site
• Hideyuki Miura Research Group

  

  Self-similar structures in nonlinear PDEs

  • Navier-Stokes equations
  • Nonlinear partial differential equations
• Kalman Laboratory

  

  Floer homology, invariants of knots and graphs

  We study geometric constructions such as Floer homology in relation to combinatorial quantities associated to knots and graphs.

  • Low dimensional topology
  • Knot theory
  • Algebraic combinatorics
• Ma Laboratory

  

  Global structure of moduli spaces

  • Moduli spaces
  • Modular forms
  • Rationality problem
• Naito Laboratory

  

  Understanding identities through representations

  Our aim is to understand identities through representations of quantum groups, by means of crystal bases; one of the main tools for the study of representations of quantum groups.

  • Representation theory of infinite-dimensional Lie algebras
  • Representation theory of quantum groups
  • Combinatorics of crystal bases
  • Symmetric Macdonald polynomials
• Onodera Laboratory

  

  Nonlinear analysis of geometric variational problems

  We investigate variational problems arising in nature and clarify their underlying principles through mathematical abstraction.

  • Partial differential equation
  • Variational problem
  • Evolution equation